단일 출발지 최단 경로 Single Source Shortest Path
Single Source Shortest Path란, 말 그대로 하나의 출발지(Single Source)에서 시작한 최단 경로(Shortest Path)를 말합니다.
다익스트라 알고리즘 Dijkstra Algorithm
Dijkstra 알고리즘은, 가중치가 있고(Weighted) 방향이 있는(Directed) 그래프에서 Single Source Shortest Path(SSSP)을 구하는 알고리즘입니다. 단, Dijkstra의 경우 가중치(Weight)가 0보다 크거나 같은 그래프만 풀 수 있습니다. Weight가 모든 범위, 즉 음수도 존재하는 그래프의 SSSP를 푸는 알고리즘으로는 벨만-포드(Bellman-Ford) 알고리즘이 있습니다.
Dijkstra 알고리즘에 사용되는 개념은 다음과 같습니다.
- Dijkstra 알고리즘은 기본적으로 BFS를 이용합니다.
- 추가 보조 자료구조로 우선순위 큐(Priority Queue)를 사용합니다.
- Edge Relaxation을 사용합니다.
아래는 Edge Relaxation의 개념이 설명되어 있는 글입니다.
[알고리즘] DAG 최단 경로 문제(DAG Shortest Path Problem)
Directed Acyclic Graph(DAG) DAG란 그래프 연결에 방향이 있고(Directed), 한 곳에서 순환이 발생하지 않는(Acyclic) 그래프(Graph)를 의미합니다. Edge Relaxation DAG Shortest Path 문제를 풀기 위해 Edge Relaxation 개념이
stevenkim1217.tistory.com
Dijkstra 알고리즘의 Pseudo Code

- Single Source 문제 이기 때문에 시작하고자 하는 하나의 vertex(root)를 0으로 초기화하고, 이외의 노드는 ∞로 초기화합니다.
- Priority Queue에서 최솟값을 추출합니다. 즉, 가장 작은 값을 가지고 있는 vertex에서
- 해당 vertex에 연결되어 있는 모든 edge에 대해 edge relaxation을 진행합니다.
Dijkstra Algorithm의 원리
Pseudo Code를 한줄 씩 따라가보며 Dijkstra 알고리즘의 진행을 보겠습니다.

- 우선 시작하고자 하는 노드(s)만을 0으로 초기화하고, 나머지 노드는 모두 무한대로 초기화합니다. 노드의 값을 무한대로 초기화 하는 이유는, 이후 취할 relaxation이 비교 후 작은 수로 업데이트 해주는 특성을 가지고 있기 때문입니다.

- 현재의 root 노드를 가지고 있는 리스트인 S를 초기화합니다.
- 마찬가지로 Priority Queue도 초기화합니다. Q에는 Graph(G)의 모든 노드 즉, 모든 vertex(V)가 들어가 있습니다.

- Q가 비어있지 않은 상태이므로
- Q에서 가장 작은 값을 추출하여
- S에 추가합니다.
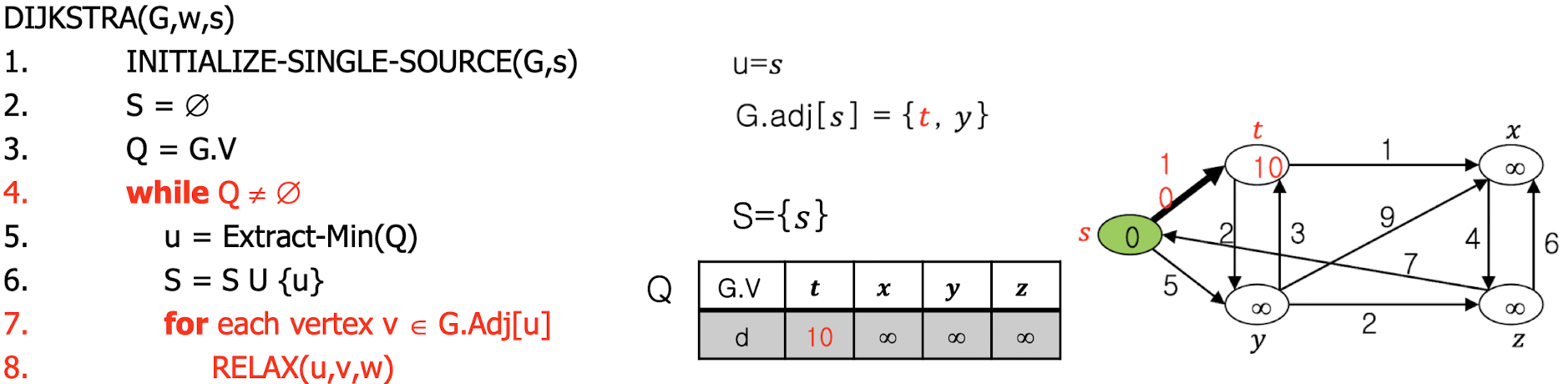
- u의 Adjacency 즉, u의 모든 인접 노드에 대해
- Relaxation을 수행합니다. 현재 t 노드에 대해 먼저 relaxation을 취해서 10<∞ 이므로, 10으로 값을 업데이트 합니다.

- 현재 u의 인접 노드 중 두번째인 y에 대해서도 relaxation을 취해줍니다.

- u에 대한 모든 인접 노드에 대해 relaxation이 끝났으므로 다음 u를 새로 추출합니다.
- Q에서 가장 작은 값을 가지고 있는 노드인 y노드가 다음 u가 됩니다.
이와 같은 방식으로 Queue가 빌 때까지 위 과정을 반복하면 다음과 같은 과정을 가집니다.

Running Time
Dijkstra 알고리즘은 Priority Queue를 구성하는 자료구조의 종류에 따라서 다른 Running Time을 가집니다. 여기서 V는 vertex의 개수를, E는 edge의 개수를 의미합니다.

- 일반 Array를 이용하여 Priority Queue를 만들면, O(V^2)의 Running Time을 가지고,

- Binary Heap을 이용하면, O[ (V+E) logV ]를,

- Fibonacci Heap을 이용하면 위 Pseudo Code의 for문(decrease_key) 부분이 상수 시간을 갖게 되어 O(E + V logV)의 값을 갖습니다.
다음은 음수의 가중치(Weight)를 가진 그래프의 Single Source Shortest Path를 찾는 알고리즘인 Bellman-Ford 알고리즘에 대한 글입니다.
[알고리즘] 벨만-포드 알고리즘(Bellman-Ford Algorithm)
단일 출발지 최단 경로 Single Source Shortest Path Single Source Shortest Path란, 말 그대로 하나의 출발지(Single Source)에서 시작한 최단 경로(Shortest Path)를 말합니다. 벨만-포드 알고리즘 Bellman-Ford Algorithm Bell
stevenkim1217.tistory.com
참고 자료
https://ocw.mit.edu/courses/6-006-introduction-to-algorithms-spring-2020/
Introduction to Algorithms | Electrical Engineering and Computer Science | MIT OpenCourseWare
This course is an introduction to mathematical modeling of computational problems, as well as common algorithms, algorithmic paradigms, and data structures used to solve these problems. It emphasizes the relationship between algorithms and programming and
ocw.mit.edu
https://ocw.snu.ac.kr/node/32373
Introduction to Algorithms | SNU OPEN COURSEWARE
ocw.snu.ac.kr
'컴퓨터 과학(Computer Science) > 알고리즘(Algorithm)' 카테고리의 다른 글
| [알고리즘] 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2023.12.01 |
|---|---|
| [알고리즘] 위상 정렬(Topological Sort) (0) | 2023.12.01 |
| [알고리즘] DAG 최단 경로 문제(DAG Shortest Path Problem) (0) | 2023.12.01 |
| [알고리즘] 깊이 우선 탐색(DFS) - Python (0) | 2023.11.10 |
| [알고리즘] 너비 우선 탐색(BFS) - Python (0) | 2023.11.10 |



