1. 병합 정렬 원리
1.1. Merge_Sort
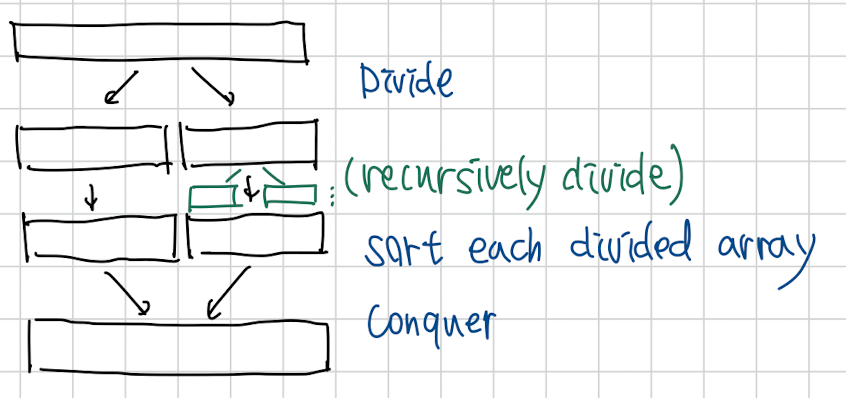
병합 정렬은 Divide and Conquer 방식을 사용합니다. 먼저 Array를 둘로 나누고(divide), 각 나눠진 Array를 각각 정렬(Conquer)하여 다시 합치는 방식을 말합니다.
이때, 재귀적으로 배열을 나누고, 정렬해주는 과정을 거칩니다.
그림으로 나타내면 아래와 같습니다.
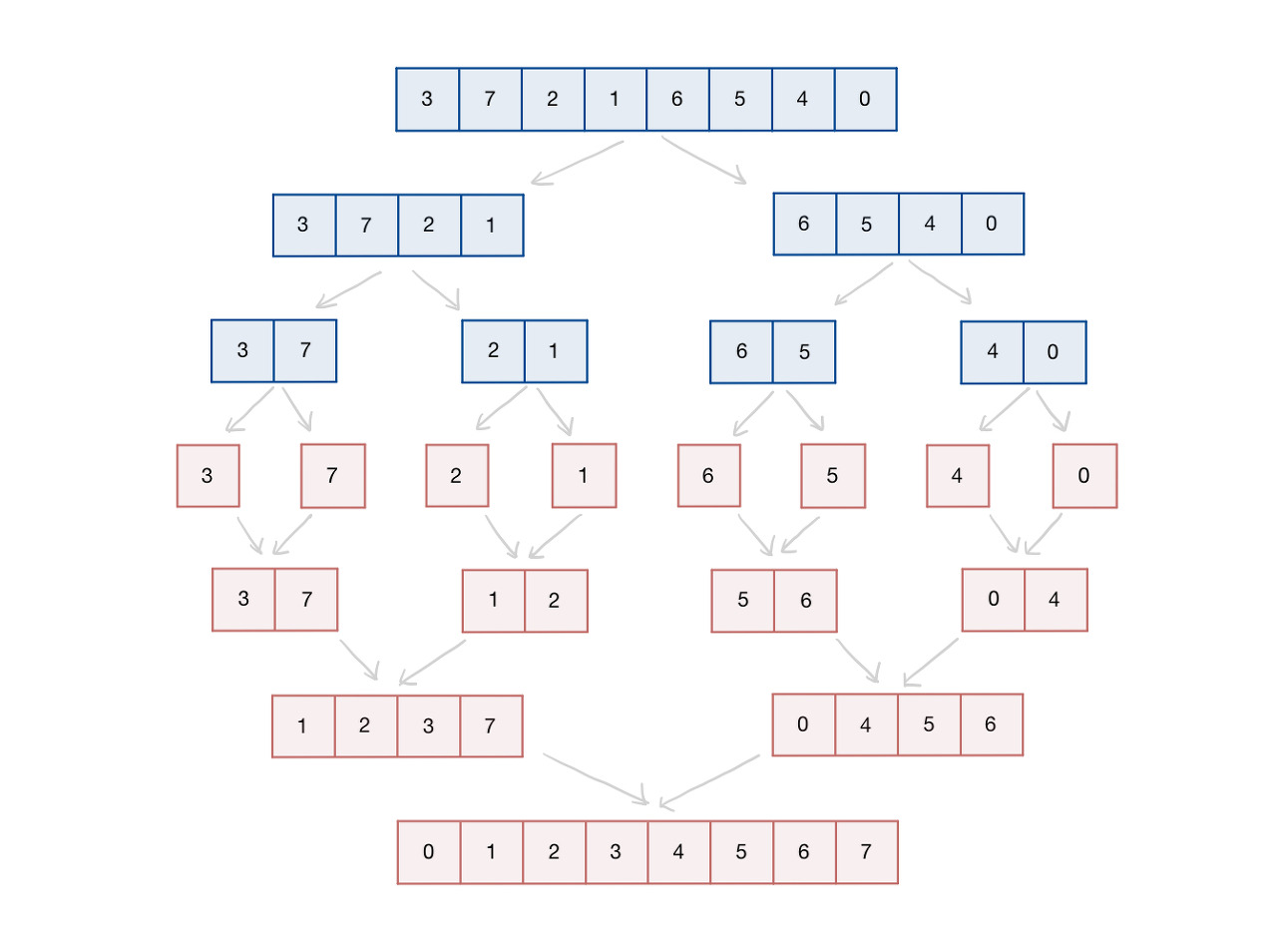
1.1. Merge
이제 각자 정렬이 끝난 두 배열을 합치는 Merge 과정을 알아보겠습니다.
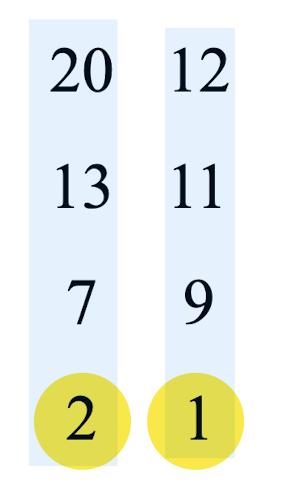
(1) 나눠져 정렬을 마친 두 배열이 왼쪽 그림과 같이 있을 때,
각 배열의 제일 앞에 있는 두 원소를 비교한다.

(2) 두 원소 중 작은 원소는 결과 list에 append한다.
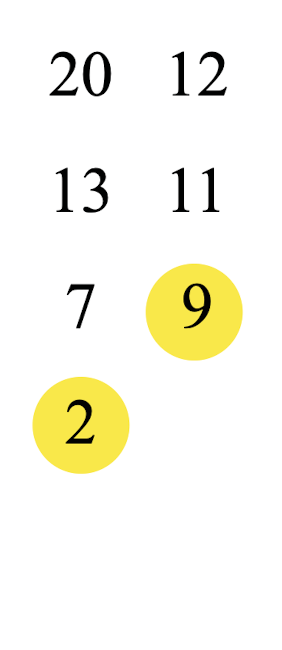
(3) list에 append된 숫자는 지우고 index를 한 칸 증가시킨다.
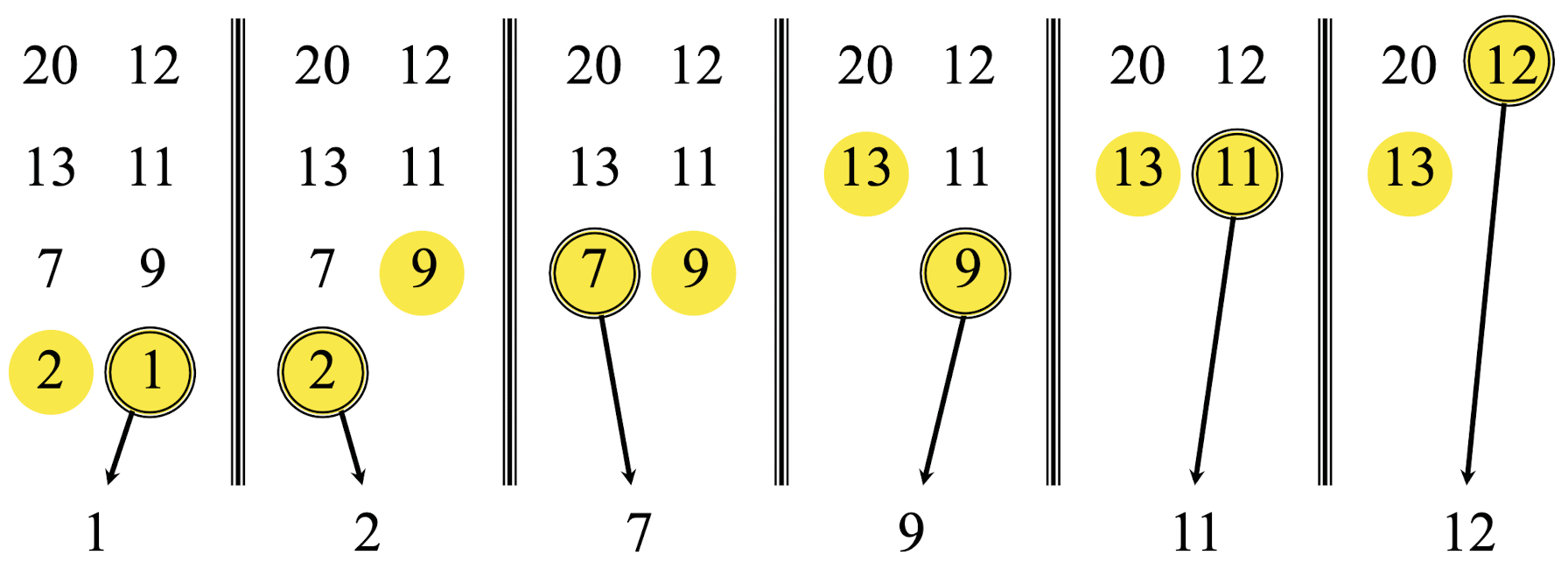
(4) 위 과정을 "하나의 Array의 원소가 다 사라질 때까지" 계속 반복한다.
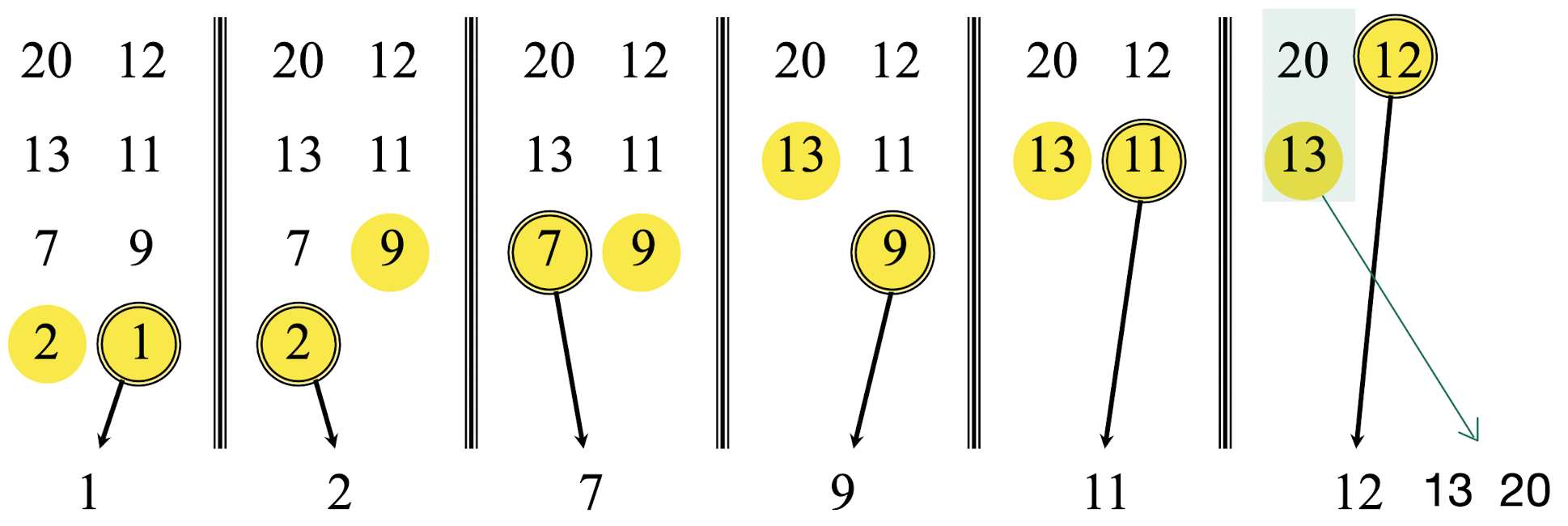
(5) 두 Array 중 하나의 원소가 모두 사라지면, 남은 한 Array의 leftover 원소를 모두 append한다.
2. 병합 정렬 Python 코드
앞서 설명한 병합 과정을 코드로 나타내보겠습니다.
result = []
i = j = 0먼저 값들을 초기화 해줍니다.
결과 array를 담을 result list를 만들고,
이후 loop에서 사용할 i,j index를 0으로 초기화합니다.
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1array를 순회하는 인덱스 i와 j가 array를 벗어나지 않는 동안,
위에서 설명한 병합과정대로, 대소 비교를 수행하여 작은 값부터 차례대로 result array에 append합니다.
result.extend(left[i:])
result.extend(right[j:])
return result마지막으로, i 또는 j 중에 하나의 인덱스가 array의 범위를 벗어나면 ( == 둘 중 하나의 array의 원소가 남지 않으면),
남은 array의 모든 원소를 Python의 extend()함수를 통해 모두 result에 append합니다.
그리고, 마지막으로 result를 return합니다.
이번에는 array를 정렬하는 Merge_sort 함수 코드에 대해서 설명하겠습니다.
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]먼저 전체 길이의 절반을 mid 변수에 할당해줍니다.
left에는 array에서 앞부분 절반을,
right에는 array에서 뒷부분 절반을 할당합니다.
left = merge_sort(left)
right = merge_sort(right)그 다음 recursive를 통해, merge sort를 계속 반복해줍니다.
return merge(left, right)마지막으로 나눠진 left와 right를 merge() 함수를 통해 병합해준 것을 반환합니다.
아래는 병합 정렬의 전체 코드 및 병합 정렬 실행시간을 나타내는 코드입니다.
Implement Merge Sort on random shuffled [1,2,3,4,5, .... 9999,10000]
import time
import random
list = list(range(1, 10001))
random.shuffle(list)
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
left = merge_sort(left)
right = merge_sort(right)
return merge(left, right)
def merge(left, right):
# L = [0]*len(left)
# R = [0]*len(right)
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] < right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
def merge_sort_time(arr):
start_time = time.time()
merge_sort(arr)
end_time = time.time()
return end_time - start_time
time_a = merge_sort_time(list)
print("merge sorting time (sec):", time_a)
# merge sorting time (sec): 0.02367377281188965
3. 병합 정렬 시간복잡도/공간복잡도
시간복잡도:
병합 정렬 전체 시간복잡도를 T(n)이라고 하면, T(n) = C(1) + 2T(n/2) + C(n) 입니다.
- C(1): Divide하는 과정은 많아봤자 n번입니다. 상수 시간을 갖습니다. 이는 작은 값이라 무시합니다.
- 2T(n/2): Recursively Sort하는 과정은 2T(n/2)의 시간을 갖습니다.
- C(n): Merge하는 과정에서 C(n)의 시간을 갖습니다.
Recursion이 일어나는 것을 시각화하면 아래와 같습니다.
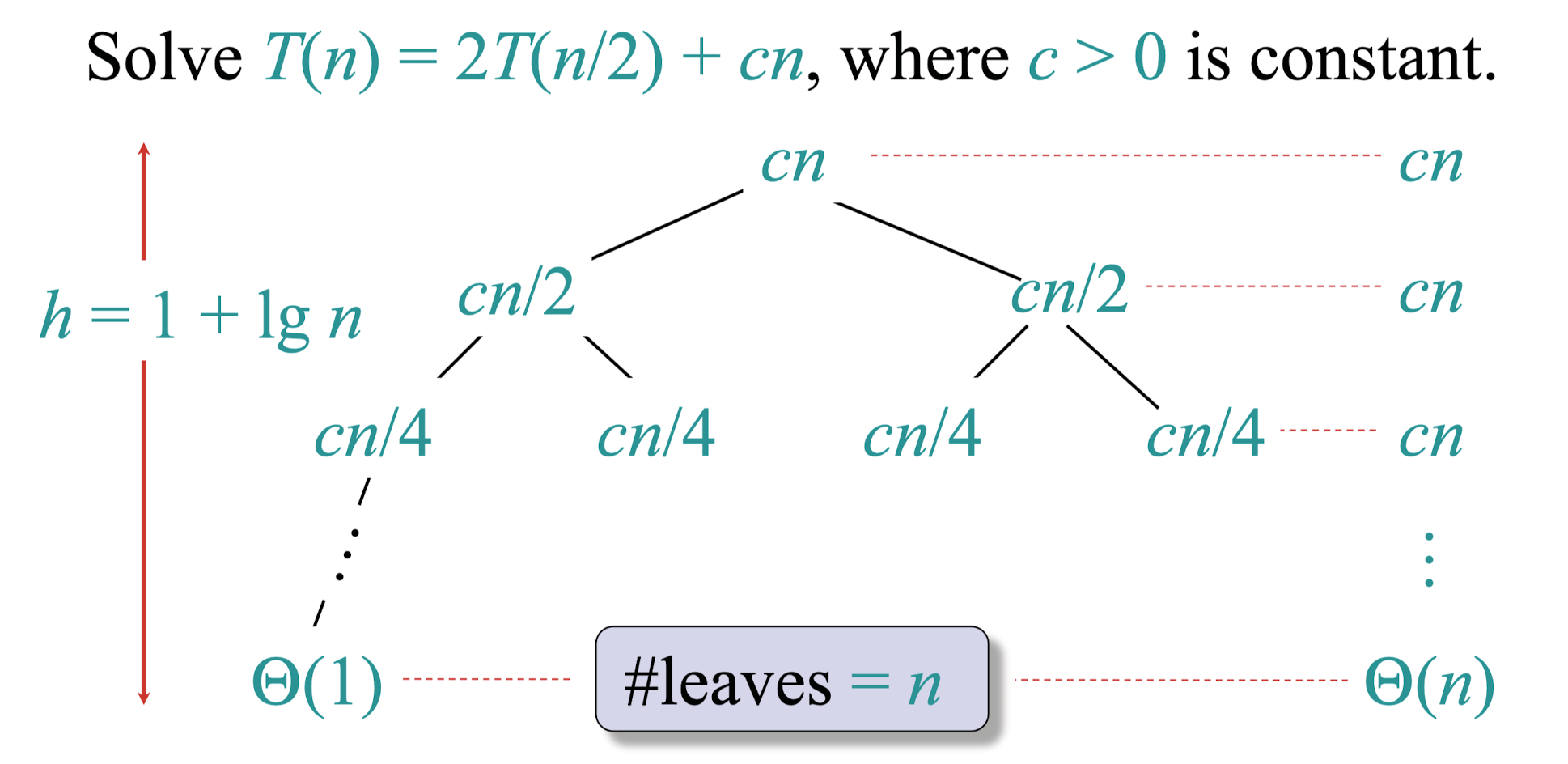
어차피 n을 쪼개는 것이기 때문에, 매 Level에서 발생하는 반복 횟수는 똑같이 cn입니다.
이진 tree의 성질에 따라 높이는 logN을 가지게 되고,
한 level에서 발생하는 cn번의 반복횟수가 총 높이인 logN만큼 반복되므로, n*log(n) = nlog(n)이 됩니다.
따라서, 병합정렬의 시간복잡도는 O(nlogn)입니다.
공간복잡도:
병합 과정에서 대소비교를 마친 값들을 추가 보조 공간(Auxiliary space)에 append하였습니다.
총 n개의 원소를 정렬하는 것이므로, 추가 공간에 들어가는 원소 또한 n개입니다.
따라서 병합정렬에는 n size의 Auxiliary Space를 필요로 합니다.
'컴퓨터 과학(Computer Science) > 알고리즘(Algorithm)' 카테고리의 다른 글
| [알고리즘] DAG 최단 경로 문제(DAG Shortest Path Problem) (0) | 2023.12.01 |
|---|---|
| [알고리즘] 깊이 우선 탐색(DFS) - Python (0) | 2023.11.10 |
| [알고리즘] 너비 우선 탐색(BFS) - Python (0) | 2023.11.10 |
| [알고리즘] 퀵 정렬 (Quick Sort) - Python (0) | 2023.10.28 |
| [알고리즘] 삽입정렬(Insertion Sort) - Python (0) | 2023.10.28 |



