1. Vector Calculus(벡터 미적분학)
Machine Learning에서는 Gradient(기울기) 개념을 자주 사용한다.
Gradient는 가장 가파른 경사의 방향을 향하기 때문에, 머신러닝 모델에서 학습을 수행하기 위해 필수적이다.
이러한 Gradient를 다루기 위해 가장 기초가 되는 도구가 Vector Calculus로, 머신러닝에서 필수적이다.
2. Objective Function(목적함수)
Machine Learining은 결국 Objective function를 최적화하는 작업이다.
이러한 최적화 작업의 일반적인 메뉴얼은 아래와 같다.
(아래 ⅰ ~ ⅲ의 과정은 모든 Machine Learning 분야에서 동일하며, 목적함수만 목적에 따라 바뀐다.)
1) 항상 초기 자료에는 노이즈(ᰚ)가 존재한다.
따라서, 우선 주어진 자료에 대해 할 수 있는 최선의 prediction은 노이즈(ᰚ)를 제외한 나머지 데이터가 될 것이다.

2) 목적함수는 다음과 같이 정의한다.
이때 우변의 식은 Error을 의미하는데, 이 Error을 minimize하는 w를 찾는 것이 목적이다.
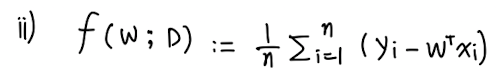
3) w 찾기는 Continuous Optimization을 이용한다.
Q: 왜 Continuous 인가요?
A: 가능한 모든 Vector에서 찾기 때문에 연속성을 띈다.
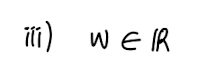
3. Function(함수)
이번 chapter에서는 function의 개념에 집중한다.
- Linear Algebra 에서의 function: Linear transformation(선형 변환) - 선형성을 띄는 1차원에서의 mapping
- Vector Caculus 에서의 function: 선형성에서 벗어난, 고차원에서의 mapping
Function은 두 quantities를 연관시키는 quantity를 말한다.
이때 두 quatities는 각각 input인 x와 target인 f(x)를 말한다.
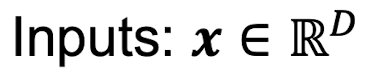
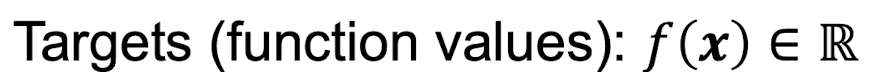
이러한 mapping을 Linear function을 이용해 표현하면 다음과 같다.

여기서 R^D를 f의 domain(정의역)이라 하고, f(x)를 f의 image(상/치역) 혹은 codomain(공역)이라 한다.
(이때, x와 f(x)는 bijective(일대일대응)이므로, image = codomain 이다.)
Example)
Linear Algebra에서 dot product는 아래와 같이 표기했다.

Vector Calculus에서의 표기 방식으로 dot product를 표기하면, 아래와 같다.
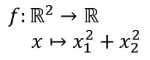
이 표기법으로 두가지 내용을 파악할 수 있다.
1) dot product는 2차원의 벡터 x를 스칼라 형태의 1차원으로 축소시키는 mapping이며,
2) vector x의 연산은 x1^2 + x2^2을 수행한다.



